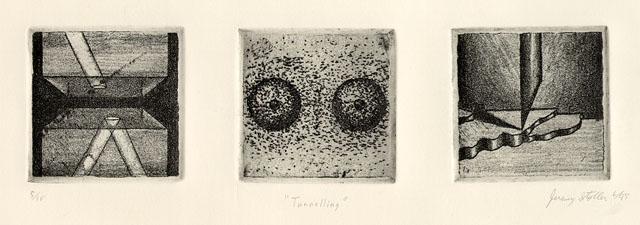
This print depicts three different examples of a phenomenon known as quantum tunneling. When a particle is trapped by a barrier, which it does not have enough energy to penetrate, there is a finite chance that particle will somehow "tunnel" through the barrier anyway. Imagine a marble rolling around the bottom of a bowl. Assume that this marble only has enough energy to roll half way up the side of the bowl. The quantum tunneling phenomenon predicts that there is a chance that the marble will suddenly appear on the outside of the bowl. In actuality, the probability of this happening with any macroscopic object, like a marble, is negligibly low. However, the theory is quite sound.

The central image in the print depicts electron tunneling. An electron orbiting an atom is analogous to the marble rolling around the bowl. There is a 90% chance that the electron will be found within its orbit shell, but that other 10% of the time the electron tunnels out side of its allowed orbit and can be anywhere else in the universe. The probability of a particle tunneling to a particular point falls off exponentially with distance however, so the electron is likely to found near (if not in) its atom. The image shows two atoms close to one another, so that electrons from one atom are likely to tunnel over to the other atom. The density of black in the image is analogous to the probability density of finding the electron.

The right hand image depicts the tip of a Scanning Tunneling Microscope, or STM, scanning a sample. This Nobel prize winning microscope uses the electron tunneling phenomena to image metallic substances on an atomic level. It does this by passing an extremely sharp wire tip within an atom's width of the sample, and monitoring the current created by electrons tunneling between the tip and the sample.

The left hand image depicts the tunneling of photons (particles of light), known as frustrated internal reflection. If you shine light through a piece of glass, when it reaches the surface some of the light will pass through, and some of the light will be reflected back into the glass. The amount of the light which gets reflected depends on the angle at which the light hits the surface of the glass. For any frequency of light, there is one critical angle at which all of the light is reflected. This is known as total internal reflection. If, however, you place a second piece of glass very close to the surface of the first, then some of the light will tunnel through the barrier between the two surfaces, and continue traveling through the second piece of glass, even at that critical angle. This is frustrated internal reflection.